First published February 2018
Key aspects to consider in the design and maintenance of an efficient modern heat storage system. We consider insulation, storage and heating temperatures, the two types of stores, overall efficiency of design and how to size a heat storage system.
Quick Links:
- Why heat storage is key to an efficient heating system
- Good heat store insulation
- High storage temperature, low heating return temperature
- Vertical stores vs. horizontal stores
- The heat store as the centre of the heating system
- How to size a heat storage system
Why heat storage is key to an efficient heating system
The fundamentals of heat storage in horticulture have not changed much since its introduction. However, modern systems are now seen more as a resource than just another functional part of a heating system. Even the language we use to refer to them reflects this. They were once referred to as ‘heat dump tanks’, whereas now they are ‘heat or thermal storage tanks’.
Finer points of the application of storage have been improved (for example, the control flow and temperature) and a wider range of heating sources has made heat storage more important in maintaining efficient operation of the whole heating system.
Growers who are thinking about, or who already have, heat storage should be aware of the characteristics and benefits, which are set out here, and be sure to specify a design which gives lowest system running costs and highest overall benefit.
Good heat store insulation
Why incorporating good thermal insulation in your heat store design makes sense.
Early heat store designs rarely incorporated good thermal insulation. The heat they contained was often regarded as a freely recovered ‘waste’, and the fact that an appreciable amount of this heat might be lost to the atmosphere was largely ignored.
Increases in the price of fuels and better controls on stored heat systems have convinced growers and installers that waste heat is just as valuable and useful as primary produced heat. Therefore, it is logical to conserve it to keep costs low.

An uninsulated 500m3 store operating at 90°C and having a surface area of 200m2 will emit heat to atmosphere at a rate in excess of 400kW in cold conditions. This is, potentially, worth over £200 per day at current gas costs and boiler efficiencies. A modest amount of insulation, for example 50mm of mineral wool matting, will reduce losses by as much as 95%.
High storage temperature, low heating return temperature
How the difference between storage and return water temperatures impacts heat store size.
Optimum heating temperatures
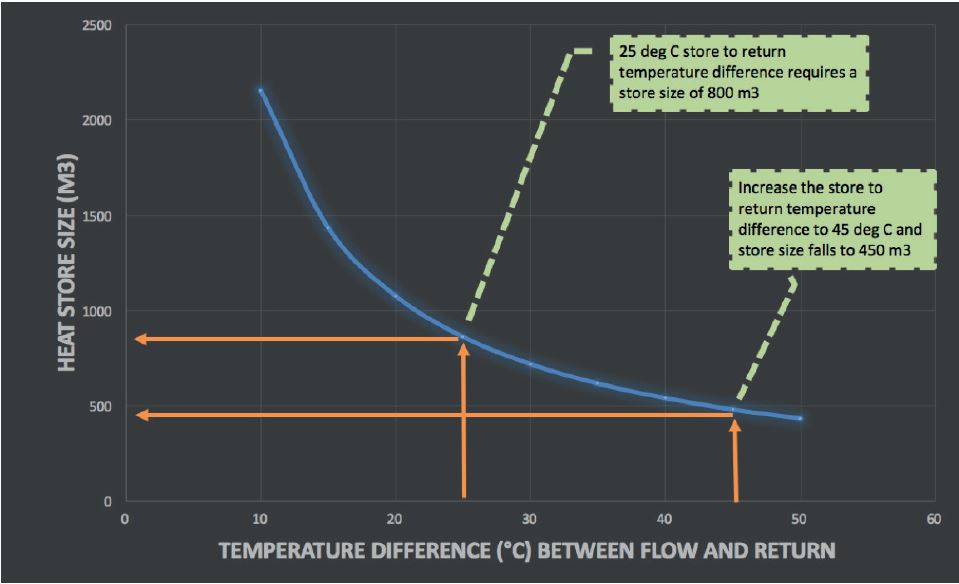
The amount of heat that can be stored in a given volume of water is proportional to the temperature difference between its fully heated state and the return temperature from the glasshouse heating system.
In the best systems, water is heated to about 90°C and returns from the glasshouse at 45°C, a difference of 45 degrees. A less well configured system might have a storage temperature of 80°C and a return temperature of 55°C, a difference of 25 degrees. The sub-optimum configuration results in 45% less heat being stored or, putting it another way, the need to increase storage by 80% to obtain the same heat storage capacity (see Figure 1).
Vertical stores vs. horizontal stores
The benefits of vertical heat stores over horizontal heat stores and their different characteristics.
The trend for higher but thinner heat stores
Most older stores were horizontal compared with newer designs, which are often upright. The trend now is to make the store higher but thinner. There is a practical limit on the height of stores of about 10 to 12 metres, because of the water pressure they exert on the heating system.
Other than for structural reasons and the occupation of less ground area, a vertical aspect has some thermal advantages too. Hot and cold water tend to separate in a container and do not naturally mix without agitation. This layering is a useful property, because, as long as the hottest water is drawn from the top and the coldest water is replaced at the bottom, the effective useful storage at the higher temperature amounts to most of the volume of the container.
However, there is some wasted volume at the level at which the hot and cold water come into contact. Here there is usually a zone of graduated temperature water, which limits the effective volume of the hot water store at high temperature. With a vertical tank, the proportion of the volume of the tank which is taken up by this temperature gradient area is reduced. In the example shown in Figure 2, wasted store volume is reduced from 15% to 3% by having a 10m high.

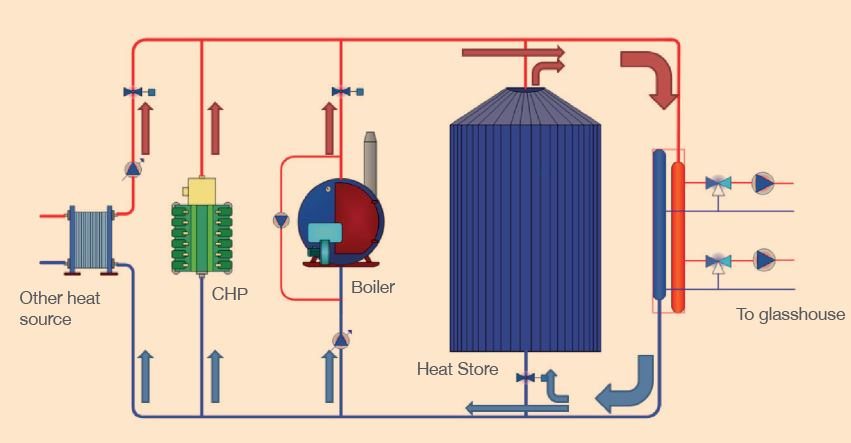
The heat store as the centre of the heating system
How to design an efficient heating system by making the heat store the preferred heat source for the system.
Optimise the use of the heat store
It is important that the control system sees the thermal store as the centre of the heating system and the place from which heat is called before a boiler or other heat generator is switched on (see Figure 3). Sometimes inefficiencies are introduced by making the boiler the ‘lead’ supplier of heat, as this compromises the ability of the store to smooth out the delivery of heat and help the boiler and other equipment operate in the most efficient way.
In this example, the heat demand of the glasshouse is being met by all heat sources, but as long as the heat store has capacity to cope, it will be the preferred heat source for the system.
How to size a heat storage system
How to calculate heat store size, related to heat demand and heat production and also assess the benefit of increasing the flow/return differential temperature.
The essential calculations
Required hot water storage volume depends on what amount of heat needs to be stored over the highest demand cycle period (normally a day) and the temperature between the flow and return pipes to and from the store.
The amount of heat storage for a water based system is given by the formula:
Q = V x (Tf – Tr) x 1.162
Where:
Q is the amount of heat stored in kWh
V is the volume of water in the tank in m3
Tf is the flow temperature from the store in °C
Tr is the return temperature to the store in °C
1.162 is derived from the specific heat capacity of water (4180J/kg°C) divided by time (3600 seconds).
By rearranging this equation, the volume of hot water needed to store a given amount of heat (Q) is given by:
V = Q / ((Tf x Tr) x 1.162)
For example, if heat required by one hectare of glass during the day is 10,000kWh and the flow and return temperatures of the store are 85°C and 55°C respectively, then the heat store size to deliver all of this heat would be:
V = 10,000 / ((85 – 55) x 1.162) = 287m3
Interestingly, the sizing ‘rule of thumb’ for heat storage for a salad crop is 200m3/Ha.
Clearly, it is important to take into consideration the highest heat demand during the period when waste heat is available. Also, note the flow and return temperatures from the store are important, as the closer they are together, the more storage is needed to deliver the same amount of heat.
When considering heat store requirement to buffer a biomass boiler, it is necessary to take into account the amount of buffering time that is required. For example, you may wish to keep a biomass boiler running for, say, two hours, even when the heat demand has disappeared, just to stop the boiler from unnecessary and inefficient cycling.
Take a 1MW boiler (1,000kW) which needs a two-hour buffer for efficient operation. Heat storage is therefore: 2 hours x 1,000kW which is 2,000kWh.
Using the equation above and based on the same flow and return temperatures, the volume of storage required would be:
V = 2000 / ((85 – 55) x 1.162) = 57m3
The rule of thumb for biomass boiler heat stores is between 50m3/MW and 100m3/MW.
The principles shown here can be used to determine store size, related to heat demand and heat production and also assess the benefit of increasing the flow/return differential temperature.

Useful Links
The basics of thermal storage for horticulture